Question

Find the x-intercept of the parabola with vertex (3,-2) and y-intercept (0,7)

Answer 1

The x-intercepts (there are 2 of them) are located at (3±√2, 0)

Explanation:

In order to find the x-intercepts, we have to factor the equation to solve it for x. However, at the present time, we have no equation to factor; we only have the vertex (h, k) and a coordinate (0, 7). So we will use those to find the equation of the parabola. If you graph the points, it's apparent that this is a positive x-squared parabola of the vertex form:

`y=a(x-h)^2+k`

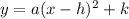
We need to solve for a to get the correct equation. Filling in our info gives us:

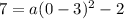`7=a(0-3)^2-2` so

7 = a(9) - 2 and

9 = 9a so

a = 1. The equation for our parabola is

`y=(x-3)^2-2`

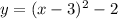
The easiest way to find the x-intercepts (factor it) is to write it in standard form which is

`y=ax^2+bx+c`

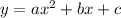
In order to do that we have to expand that binomial by FOILing and we get

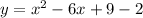`y=x^2-6x+9-2` which simplifies to

`y=x^2-6x+7`

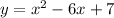
In order to factor that you have to throw it into the quadratic formula. That looks like this:

`x=(6+/-√(-6^2-4(1)(7)) )/(2(1))`

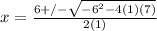
which simplifies to

`x=(6+/-√(8) )/(2)`

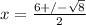
The square root of 8 simplifies:

`x=(6+/-2√(2) )/(2)`

and dividing everything but the radicand (the number under the square root) by 2 gives you both of your x-intercepts:

x = 3 ± √2