Question

20 points! Can someone do part A for me? I know how to do these questions I’m just a tad bit confused. :/

Answer 1

revenue = (number of phones)(price of phones)

If Mobistar charges $80 per phone, then their revenue is


`r=800*80=64,000`

If they instead charge $2 less per phone (so that
`d=1`), or $78 per phone, then their revenue would be


`r=840*78=65,520`

If they charge $4 less per phone (
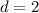
`d=2`), then they make


`r=880*76=66,880`

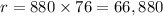
and so on. As the hint suggests, we can write the number of phones sold as an expression depending on the number of price decreases
`d`; that is, for each price decrease, the number of phones sold increases by 40.

Similarly, the price per phone can be written in terms of
`d`, since the cost of a phone starts at a fixed $80 and decreases by $2 for each unit of
`d`. So total revenue can be written as


`r(d)=(800+40d)(80-2d)`

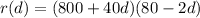
You can stop there, but you may be expected to write this in standard quadratic form, which is just a matter of expanding
`r(d)`.


`r(d)=64,000+1,600d-80d^2`

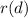
For the remaining parts:

(B) Writing in vertex form will help, as the name suggests. That's just a matter of completing the square. You have


`r(d)=-80d^2+1,600d+64,000`

`r(d)=-80(d^2-20d-800)`

`r(d)=-80(d^2-20d+100-100-800)`

`r(d)=-80((d-10)^2-900)`

`r(d)=72,000-80(d-10)^2`

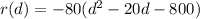
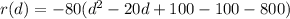
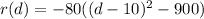
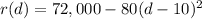
which is to say the vertex of the parabola described by
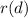
`r(d)` occurs at (10, 72,000). The parabola "opens downward" (which we know because the sign of the leading (quadratic) term is negative), so the vertex is a maximum of the revenue function, which in turn means the most revenue the company can achieve will be achieved if
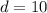
`d=10`, netting them $72,000. This translates to setting the price per phone to
`80-2(10)=\$60`.