Answer:
Explanation:
In the given figure we have two triangles (One into another).
In triangle BDE,
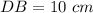
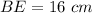
In triangle ABC,
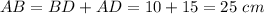
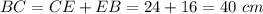
Now, in ΔABC and ΔBDE , we have
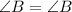 [Reflexive property]
[Reflexive property]
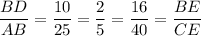
By SAS Similarity Theorem ,
ΔDBE is similar to ΔABC
- SAS Similarity Theorem say that if two sides in a triangle are proportional to two sides in another triangle and the included angle in both are congruent then the two triangles are said to be similar.