If this is your equation

, then I would add the two fraction of the left by getting the LCD (lowest or least common denominator after which I would use cross-product. (Whispers you could just plug in the answer choices to see which one works)
Back to work: LCD of 2 and 2x is 2x
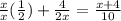

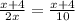
←after adding the fractions did you notice that the numerators are equal therefore the denominators must be equal
2x = 10
x = 5 when you divide both sides by 2... please check your answer