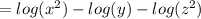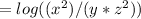Final answer:
To write the expression
 as a single logarithm, we can combine the terms using logarithmic properties. The expression can be simplified to
as a single logarithm, we can combine the terms using logarithmic properties. The expression can be simplified to
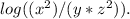
Step-by-step explanation:
To write the expression
 as a single logarithm, we can use the properties of logarithms to combine the terms.
as a single logarithm, we can use the properties of logarithms to combine the terms.
First, applying the property of division, log(x/y) can be written as
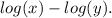
Next, applying the property of multiplication, log(a*b) can be written as log(a) + log(b).
Finally, combining all the terms, we have: