Using the definition of the Laplace transform:
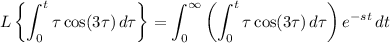
Reverse the order of integration. In the
 plane, the domain of integration can be expressed as given,
plane, the domain of integration can be expressed as given,
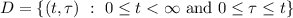
or equivalently as
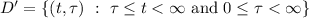
Then the Laplace transform is
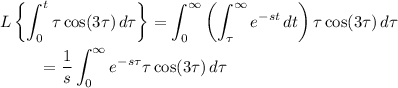
and the remaining integral is exactly the Laplace transform of
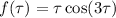 , which can be easily if tediously computed by parts, or you can look it up in a transform table. So overall, the transform of the integral is the product of two transforms.
, which can be easily if tediously computed by parts, or you can look it up in a transform table. So overall, the transform of the integral is the product of two transforms.
This is equivalent to the convolution property of the Laplace transform,
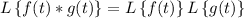
where
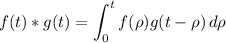
In our case, we let
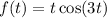 and
and
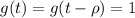 .
.