Question

Maximize:
z= 6x +12y
subject to: 4x + 5y ≤20
8x + y ≤ 20
x≥0, y 20

Answer 1

48

Explanation:

Given:

`\textsf{Maximize}: \quad z=6x+12y`

`\begin{aligned}&\textsf{Subject to}: \quad &4x+5y & \leq 20\\&&8x+y &\leq 20\\&&x\geq 0, y&\geq 0\end{aligned}`

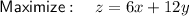
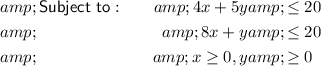
Graph the lines:

`\textsf{Draw the line } \;\;4x+5y=20 \;\;\textsf{and shade under the line}.`

`\textsf{Draw the line } \;\;8x+y=20 \;\;\textsf{and shade under the line}.`

`\textsf{Draw the line } \;\;x=0\;\;\textsf{and shade above the line}.`

`\textsf{Draw the line } \;\;y=0\;\;\textsf{and shade above (to the right of) the line}.`

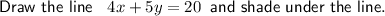
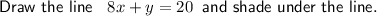
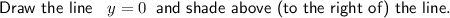
Therefore, the feasible region is bounded by the corner points:

• A = (0, 0)
• B = (0, 4)
• C = (⁵/₂, 0)
• D = (²⁰/₉, ²⁰/₉)

Determine the value of z at the corner points by substituting the x and y values of the points into the equation for z:

`\textsf{Value of $z$ at $A(0,0)$}: \quad 6(0)+12(0)=0`

`\textsf{Value of $z$ at $B(0,4)$}: \quad 6(0)+12(4)=48`

`\textsf{Value of $z$ at $C\left((5)/(2),0\right)$}: \quad 6\left((5)/(2)\right)+12(0)=15`

`\textsf{Value of $z$ at $D\left((20)/(9),(20)/(9)\right)$}: \quad 6\left((20)/(9)\right)+12\left((20)/(9)\right)=40`

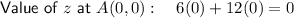
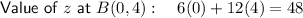
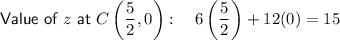
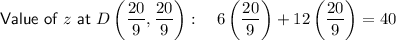
Hence, the maximum value of z is 48 at B(0, 4).