Answer:
A.
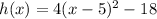
Explanation:
We have been given an equation of a function
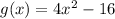 . We are asked to find the formula of the function our g(x) is shifted 5 units to the right and 2 units down.
. We are asked to find the formula of the function our g(x) is shifted 5 units to the right and 2 units down.
Let us recall the transformation rules.
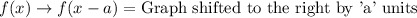
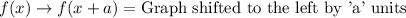
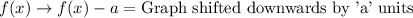
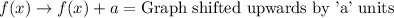
Upon shifting our function to the right by 5 units our function would be:
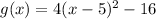
Let us shift our given function downwards by 2 units.
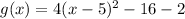
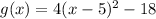
Therefore, option A is the correct choice.