Question

circles p and q have radii 6 and 2 and are tangent to each other. find the length of their common external tangent ab

Answer 1

4
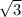`√(3)` 0r 6.93 units

Explanation:

Let's draw the figure using the given information.

Draw a perpendicular line from the center of the smaller circle to radius of bigger circle. Then it forms a rectangle with x by 2.

As you can see it formed a right triangle with the base x, legs measures 4 and 8 (6 + 2).

Now we can find the value of the base (x) using the Pythagorean theorem.

The values of x is the same as the length of external tangent AB.

The Pythagorean theorem states the square of the hypotenuse is equal the sum of the squares of their legs.

So,
`8^2 = x^2 + 4^2`

`x^2 + 16 = 64`

`x^2 = 64 -16\\x^2 = 48`

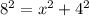
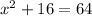
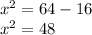
Taking square on both sides, we get

x =
`√(16*3)`

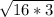
x = 4
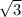`√(3)` 0r 6.93 units

Therefore, the length of external tangent AB is 4
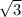`√(3)` 0r 6.93 units

Answer 2

Refer to the diagram shown below.

x = the length of the common tangent to the two circles.
From the Pythagorean Theorem,
x² + 4² = 6²
x² = 6² - 4² = 36 - 16 = 20
x = √(4)(5) = 2√5 = 4.472

Answer: 2√5 or 4.472