Answer:
Volume(V) of a circular cone is given by :
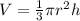 ......[1] where r is the radius and h is height of the cone respectively.
......[1] where r is the radius and h is height of the cone respectively.
Given: Radius of cone(r) = 16 cm and height of cone(h) = 8 cm

or
r =2h
Substitute in [1]; we have
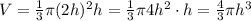 ......[2]
......[2]
It is also, given the rate
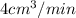 i.e,
i.e,
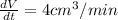
Differentiate V with respect to t in equation [2] we get;

{
 }
}
To find the rate of depth of the water when tank is 6 cm deep.
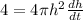
Simplify:
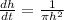
Substitute h = 6 cm we have;

or
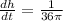 [Use
[Use
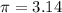 ]
]
Simplify:
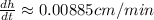
Therefore, the rate of depth of the water changing is,
