Question

a line k passes through the points-7,-14 and 1,26 a second line h passes through points -4,-25 and 4,15. is line k parallel to line h? why or why not?

Answer 1

See, pls, the following:
WAY №1 (based on properties of lines)
1) it is possible to find out an equation for line 'k' using its points (common equation for line is y=ax+b):

`\left \{ {{-14=(-7)*a+b} \atop {26=1*a+b}} \right. \ =\ \textgreater \ \ \left \{{{b=21} \atop {a=5}} \right.`
this means, for line 'k' y=5x+21
2) for line 'h' (the same operations):

`\left \{ {{-25=-4*a+b} \atop {15=4*a+b}} \right. =\ \textgreater \ \ \left \{ {{a=5} \atop {b=-5}} \right.`
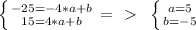
equation for line 'h' is y=5x-5
The parameter 'a' for the both lines is the same, it means k║h.
WAY №2. (based on properties of vectors):
1) find points for vector 'k': (1--7;26--14) ⇒ (8;40).
2) to do the same for vector 'h': (4--4;15--25) ⇒ (8;40).
3) using the found points for the both vectors to compare them:

`(8)/(8) =1 \ and \ (40)/(40)=1`
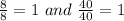
1=1 it means the both lines are parallel.