Answer:
The distance between the slits is given by 1.3 ×
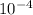 m
m
Given:

D = 4 m
y =
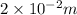
m = 1
To find:
distance between slits, d = ?
Formula used:
y =
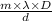
y = distance of first bright band from central maxima
D = distance between screen and source
d = distance between slits
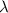 = wavelength
= wavelength
Solution:
distance of first bright band from central maxima is given by,
y =
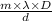
y = distance of first bright band from central maxima
D = distance between screen and source
d = distance between slits
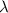 = wavelength
= wavelength
Thus,
d =

d =
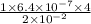
d = 1.28 ×
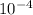
d = 1.3 ×
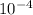 m
m
The distance between the slits is given by 1.3 ×
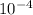 m
m