Question

Matt flips $100$ coins. those that land heads, he sets aside. he then reflips the coins that landed tails, and again sets aside all those that land heads. finally, he flips a third time the coins that landed tails twice, and again sets aside all those that land heads.what is the expected number of coins matt sets aside?

Answer 1

Let X be the random variable representing the number
of coins that Matt set aside after three flips.

`P(X_1=n)=P(B(100,(1)/(2))=n),\text{ B is the binomial distribution.}\\P(X_2=m)=P(B(100-n,(1)/(2))=m)\\ P(X_3=l)=P(B(100-n-m,(1)/(2))=l)`
We have to run n from 0 to 100 and m from 0 to (100-n),
Find the binomial law, then compute the mean like this:

`(100-n-m)/(2)`
Hope this gives a hint.

Answer 2

The theoretical probability that flipped coin lands head is
`(1)/(2)` ahd the theoretical probability that flipped coin lands tail is also
`(1)/(2).`

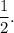
1. Matt flips 100 coins, those that land heads, he sets aside. Count how many coins theoretically land heads:

`100\cdot (1)/(2)=50.`

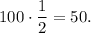
Then he sets 50 coins aside and 50 coins that land tails left.

2. Matt flips 50 coins, those that land heads, he sets aside. Count how many coins theoretically land heads:

`50\cdot (1)/(2)=25.`

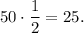
Then he sets 25 coins aside and 25 coins that land tails left.

3. Matt flips 25 coins, those that land heads, he sets aside. Count how many coins theoretically land heads:

`25\cdot (1)/(2)=12.5.`

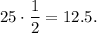
Then he sets 12 or 13 coins aside and 13 or 12 coins that land tails left.

4. In total he sets aside 50+25+12=87 or 50+25+13=88 coins.

Answer: about 87 or 88 coins he sets aside.