Question

A 12-foot ladder is leaning against a wall. The distance from the base of the wall to the base of the ladder is (square root 2 to the 6th power) feet. Given this information, what can be determined about the triangle formed by the ground, wall, and ladder?

Answer 1

The answers are A,B,D and E. Have a lovely day.

Answer 2

Length of ladder = 12 foot

`\text{Distance from the base of wall to the base of ladder = }(√(2))^6`

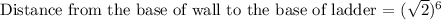
Now, since, the height of the wall and the ground's surface are perpendicular to each other.

Thus the triangle thus formed will be a right angled triangle.

Where Hypotenuse = 12 foot

`\text{Length of base = }(√(2))^6=8\:\:foot`

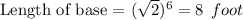
By applying Pythagoras theorem ,

`\text{height of the wall = }√(144 - 64)=√(80)\:\:foot`