Question

2. A car travels 50 km/h for 3000 meters to its destination. How long did car travel to reach its destination?

Answer 1

0.06 h or 3.6 minutes

Step-by-step explanation:

First convert 3000 meters to kilometers, because speed is also in that unit (km/h)

distance:
`s = 3000 m = 3 km`

speed:
`v = 50 km/h`

time:
`t = (s)/(v)`

Substitute in and solve:

`t = (3 km)/(50 (km)/(h) )`

`t = (3)/(50) h`

`t = 0.06 h` or
`3.6 min` (0.06 h * 60 min/h)

Answer 2

Suppose we know the formula of speed:

`\displaystyle{v=(s)/(t)}`

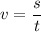
Where v = speed, s = distance and t = time.

We can solve the equation for time by first multiplying both sides by t:

`\displaystyle{v\cdot t = (s)/(t) \cdot t}\\\\\displaystyle{vt = s}`

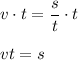
This results in distance equation but that’s not what we want for now. Divide both sides by v:

`\displaystyle{(vt)/(v)=(s)/(v)}\\\\\displaystyle{t=(s)/(v)}`

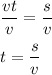
Finally, we have the time equation as shown above.

From the question, we know that v (speed) = 50 km/h and s (distance) = 3000 meters. However, since speed and distance both have different unit, we will have to change from meters to kilometers.

We know that a kilometer equals 1000 meters. Therefore, 3000 meters equal to 3 kilometers. Therefore, our new value of distance (s) is 3 kilometers.

Apply the time equation by substituting v = 50 and s = 3:

`\displaystyle{t=\frac{3 \ \, \sf{km}}{50 \ \, \sf{km/h}}}\\\\ \displaystyle{t=\frac{3\cdot 2 \ \, \sf{km}}{50\cdot 2 \ \, \sf{km/h}}}\\\\\displaystyle{t=\frac{6 \ \, \sf{km}}{100 \ \, \sf{km/h}}}\\\\\displaystyle{t=0.06 \ \, \sf{h}}`

Generally, time must be in second unit. Therefore, we’ll convert from hour to second.

We know that an hour equals to 60 minutes and a minute equals to 60 seconds. Therefore, an hour equals to 60 x 60 seconds = 3600 seconds.

Thus, 0.06 hour will equal to 3600 x 0.06 which equals to 216 seconds. Therefore, it’ll take 216 seconds to reach the destination.