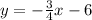Question

The equation of line l is 3x-4y=24.the line intersects x axis at a and y axis at b. Given that m is the point (4,-3) and o is the origin .find

A) the gradient of l
B)the length of ab
C)the equation of the line passing through b and having same gradient as om

Answer 1

4y=3x-24
y=3/4x-6

the line intersect x axis in A
y=0, 3/4x=6, 3x=24, x=8 ⇒ A (8,0)

the line intersect y axis in B
x=0, y=-6 ⇒ B (0,- 6)

a.the gradient of l is 3/4
b. AB= V 6^2 +8^2=V36+64=V100=10

Answer 2

note, x-axis at a, therefore coordinates is (a, 0).
y-axis at b, therefore (0, b)

a) gradient of I can be found by converting 3x-4y=24 into eqn of y=mx+c (just some simple manipulation.)
3x-4y=24
-4y=-3x+24
4y=3x-24
( ÷ by 4)
y=(3/4)x-6

gradient is hence, 3/4.

b) length of AB,
substitute y=0 into equation of line I to find point a, and separately x=0 to find point b.

once you've found the full coordinates, you may insert the values into this formula to find length of line segment.

`√((y1 - y2) + (x1 - x2))`
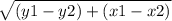
if my workings are not wrong, you should find that a=8 and b=-6 and the length is 10 units.

c) equation of line passing through b, grad = OM

find gradient OM, which is

`( - 3 + 0)/( 4 - 0) = ( - 3)/(4)`
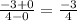
from this, substitute points b (0,-6) into
y=mx + c in order to find the 'c' constant. once, you've found the c, simply insert that c value along with the gradient of OM into y=mx+c

therefore,

`y = - (3)/(4) x - 6`