Question

M men and w women seat themselves at random in m+w seats arranged in a row. find the probability that all the women will be adjacent.

Answer 1

The correct answer is:

`((m+1)!w!)/((m+w)!)`

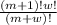
Step-by-step explanation:

We want all w women to be seated together. There are w! ways to do this.

Since all women are seated together, we consider the as 1 block to be seated with the men.

There are m! ways of arranging the men. However, we also have the 1 block of women to seat; this makes (m+1)! ways to seat the men and block of women.

There are (m+w)! ways to arrange all of the men and women.

This makes our probability

`((m+1)!w!)/((m+w)!)`.

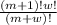For example, if there are 4 men and 3 women:

There are 3! = 6 ways to seat the women together. This makes 1 block of women.

There are 4! = 24 ways to seat the men together. Taking this with the block of women, we have (4+1)! = 5! = 120 ways to seat the men and block of women.

There are (4+3)! = 7! = 5040 ways to arrange 7 people.

This makes our probability 120(6)/5040 = 720/5040.