Answer:
Options 1 and 2 are correct.
Explanation:
The graph represents the function
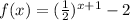
From the given graph it is noticed that the value of f(x) approaches to infinity as x approaches to negative infinity and the value of f(x) approaches to -2 as x approaches to positive infinity.
It can also represented by limits.
As x increases without bound
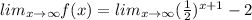
Apply limit.
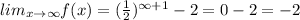
As x decreases without bound
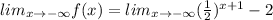
Apply limit.
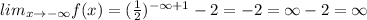
Therefore as x decreases without bound, f(x) increases without bound and as x increases without bound, f(x) approaches the line y=−2. Options 1 and 2 are correct.