Answer:
(a) By the ideal gas law, the temperature of the gas is approximately 423.51129 K
(b) By the Van der Waals equation, the temperature of the gas is approximately 442.00558 K
Step-by-step explanation:
The given parameters are;
The mass of the methane gas, m = 60 g
The volume of the container in which the gas is placed, V = 1.00-L
The pressure of the gas in the container, P = 130 atm
The molar mass of methane, CH₄ = 16.04 g/mol
The Van der Waals Constant for Methane (CH₄) a = 2.253 atm L²·mole⁻² and b = 0.04278 L·mol⁻¹
The universal gas constant, R = 0.08206 L·atm·mol⁻¹·K⁻¹
The number of moles of methane present, n = 60.0 g/(16.04 g/mol) ≈ 3.7406 48 moles
(a) The ideal gas law is P·V = n·R·T
Where;
P = The pressure of the gas
V = The volume of the gas
R = The universal gas constant
T = The temperature of the gas
n = The number of moles of the gas
Therefore, T = P·V/n·R
By substituting the known values of the variables, we get;
T = 130×1/(3.740648 × 0.08206) ≈ 423.51129 K
The temperature of the gas, T ≈ 423.51129 K
(b) The Van der Waals equation of state;
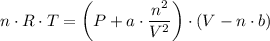
Therefore, we have;

Therefore, we have;
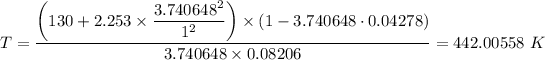
The temperature of the gas, T ≈ 442.00558 K.