Answer:
1)
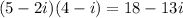
2)
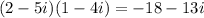
3)
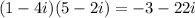
4)
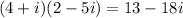
Explanation:
Given : Complex numbers
1) (5-2i)(4-i)
2) (2-5i)(1-4i)
3) (1-4i)(5-2i)
4) (4+i)(2-5i)
To find : The products of complex numbers with their standard forms.
Solution :
We simply apply multiplicative property of brackets,
i.e,
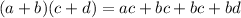
Note -
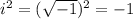
1) (5-2i)(4-i)
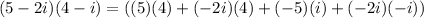
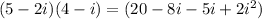
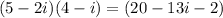
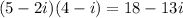
2) (2-5i)(1-4i)
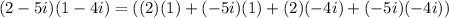
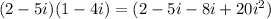
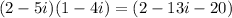
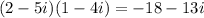
3) (1-4i)(5-2i)
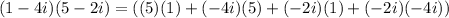
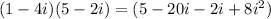
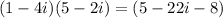
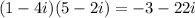
4) (4+i)(2-5i)
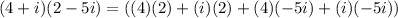
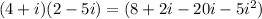
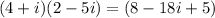
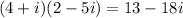
Therefore, following above are the required results.