Question

A building has a ramp to its front doors to accommodate the handicapped. if the distance from the building to the end of the ramp is 20 feet and the height from the ground to the front doors is 6 feet, how long is the ramp? (round to the nearest tenth.)

Answer 1

The ramp is 20.9 ft according to the Pythagorean Theorem.
a^2 + b^2 = c^2 when a=20, b=6, and c is the height of the ramp.

Answer 2

The answer would be:

20.9 ft

Here is why:

If you draw the scenario, (which is attached below) you can see that a right triangle is formed. The ramp length is the hypotenuse of the scenario. To solve for it, we can use the Pythagorean Theorem where:

`c^(2)= a^(2) + b^(2)`

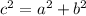
Where:

c = hypotenuse (Longest side)

a and b = legs of the triangle

Let's take our given and put it into the formula:

c = length of the ramp

a = 6ft

b = 20ft

`c^(2)= (6ft)^(2) + (20ft)^(2)`

`c^(2)= 36ft^(2)+ 400ft^(2)`

`c^(2)= 36ft^(2)+ 400^(2)`

`\sqrt{c^(2) } = \sqrt{436ft^(2)}`

`c= 20.9ft`

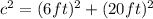
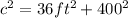
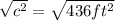
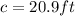
Hope you get it!