Question

a rectangular field has an area of 1452 square feet. if the width is three times greater than the length, what is the length of the field

Answer 1

width=3x
length=x
Area of a rectangle=length x width
We have to solve the following equation.
x(3x)=1452
3x²=1452
x²=1452/3
x²=484
x=+√484=22

length=x=22 feet
width=3x=3(22 feet)=66 feet.

Answer: the length of the field would be 66 feet.

Answer 2

The length of the rectangular field is 22 feets.

Explanation:

Let us write
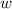`w` for the width and
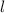`l` for the length.

From the data we know that
`w=3l`.

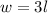By the formula of the area of a rectangle
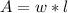`A=w*l`. Then, substituting
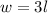`w=3l` into the formula for the area:
`A=3l^2`.

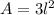So, we have the equation
`1452=3l^2`, which is equivalent to
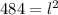`484=l^2`. Then, taking square roots in both sides:
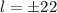`l=\pm 22`, but as we are looking for a measure we discard the negative solution. Therefore,
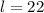`l=22` feets.