Question

The area of the smallest equilateral triangle with one vertex on each of the sides of the right triangle with side lengths and
`$2√(3),~5,$ and $√(37),$`as shown, is
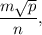
`$(m√(p))/(n),$` where m, n, and p are positive integers, m and n are relatively prime, and p is not divisible by the square of any prime. What is m + n + p?

Answer 1

Hey there,

Your correct answer final answer to this question would be 145.

Hope this helps.

~Jurgen

Answer 2

Set up the given triangle on x-y coordinates with right angle at (0,0). So the two vertices are at (5,0) and (0,2
`sqrt{x} n]{3}`)

let (a,0) and (0,b) be two vertices of the equilateral triangle. So the third vertex must be at
`((a+√(3)b)/(2) , (b+√(3)a)/(2) )`

for a pt (x,y) on line sx+ty=1, the minimum of
`\sqrt{x^(2) + {y^(2) }`
equals to
`\frac{1}{ \sqrt{ s^(2) + t^(2) } }`

smallest value happens at
`(10 √(3) )/(67)`

so area is
`(75√(3))/(67)`

hence m=75, n=67, p=3
m+n+p = 75+67+3 = 145