Question

Choose the linear inequality that describes the graph. The gray area represents the shaded region.

4x + y < 4
4x + y > 4
4x – y ≥ 4
4x + y ≥ 4

Answer 1

4x + y > 4 Should be you're answer.....

Answer 2

Answer: 4x + y ≥ 4

Explanation:

By the given graph,

The x-intercept of the line is , (1,0)

And, the y-intercept of the line is, (0,4)

Thus, the relation equation of the inequality,

`y - 0 = (4-0)/(0-1) (x-1)`

⇒
`y = (4)/(-1) (x-1)`

⇒
`- y = 4(x-1)`

⇒
`-y = 4x - 4`

⇒
`4x - 4 + y = 0`

⇒
`4x + y = 4`

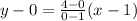
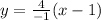
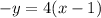
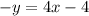
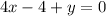
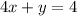
Again, by the graph the inequality does not contain the origin.

Therefore, the possible inequalities are, 4x + y > 4 and 4x + y ≥ 4

Also, the line of related equation in the graph is a solid line,

⇒ The inequalities must hold the sign ≥.

Thus, the required inequality that shown in the given graph is,

4x + y ≥ 4

⇒ Fourth option is correct.