We have been given a diagram of triangle ABC, where line segment AD is the angle bisector of ∠BAC. We are asked to find the length of segment BD.
We know that angle bisector of triangle divides the opposite side of triangle into segments that are proportional to other two sides.
Using angle bisector theorem, we will get:
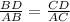
Upon substituting our given values in above equation, we will get:
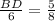
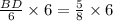
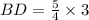
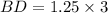
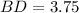
Therefore, the length of line segment BD is 3.75 units.