The remainder theorem says that the remainder upon dividing a polynomial
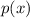
by a linear polynomial
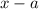
is the same as the value of
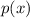
at

. Dividing by any linear polynomial will always result in the following:

where
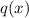
and
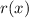
are also polynomials. Taking

, the term involving
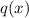
vanishes, so that

is exactly the remainder upon dividing.
Via synthetic division, we have
... | 2 -9 7 -5 11
4 | 8 -4 12 28
- - - - - - - - - - - - - - - - - -
... | 2 -1 3 7 39
which translates to
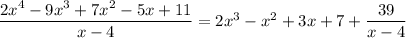
that is, we're left with a remainder of 39.
Via the remainder theorem, we have
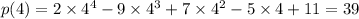
as expected.