Question

a blow dart is fired horizontally from a heght of 1.2 m if the dart hits a target that is 0.6 m high and 12m away what is the initial velocity of the dart

Answer 1

its 0.7 i know this because i did the quiz

Answer 2

Approximately
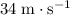`34\; {\rm m\cdot s^(-1)}` (assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

Step-by-step explanation:

Assume that the drag on the dart is negligible. Vertically, this dart will be accelerating downward at
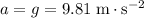`a = g = 9.81\; {\rm m\cdot s^(-2)}` under the gravitational pull.

Since this dart was launched horizontally, the initial vertical velocity of this dart will be
`u = 0\; {\rm m\cdot s^(-1)}`.

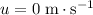The height of the dart has changed by
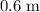`0.6\; {\rm m}`. Thus, the vertical displacement of this dart will be
`x = 0.6\; {\rm m}`.

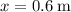Let
`t` denote the amount of time the dart spent in the air. Since the acceleration is constant in the vertical component, the SUVAT equation
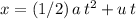`x = (1/2)\, a\, t^(2) + u\, t` would apply in that component:

`x = (1/2)\, a\, t^(2) + u\, t`.

`(0.6) = (1/2)\, (9.81)\, t^(2) + (0) \, t`.

`(0.6) = (1/2)\, (9.81)\, t^(2)`.

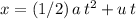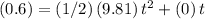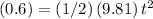Note that the term
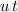`u\, t` is eliminated since the initial vertical velocity of this dart is
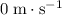`0\; {\rm m\cdot s^(-1)}` as the dart was launched horizontally.

Rearrange and solve this equation for
`t`:

`\begin{aligned} (0.6) = (1)/(2)\, (9.81)\, t^(2)\end{aligned}`.

`\begin{aligned} (1)/(2)\, (9.81)\, t^(2) = (0.6)\end{aligned}`.

`\begin{aligned} (9.81)\, t^(2) = (2)\, (0.6)\end{aligned}`.

`\begin{aligned} t^(2) = ((2)\, (0.6))/((9.81))\end{aligned}`.

`\begin{aligned} t &= \sqrt{((2)\, (0.6))/((9.81))} \\ &\approx 0.349\end{aligned}`.

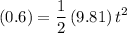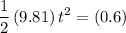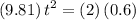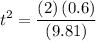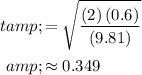Thus, it would have taken this dart approximately
`0.349\; {\rm s}` to travel from where it was launched to where it landed. Since the dart has travelled a horizontal distance of
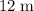`12\; {\rm m}` in that amount of time, the initial horizontal velocity of this dart would be:

`\begin{aligned}(\text{horizontal velocity}) &= \frac{(\text{horizontal displacement})}{(\text{time taken})} \\ &\approx \frac{12\; {\rm m}}{0.349\; {\rm s}} \\&\approx 34\; {\rm m \cdot s^(-1)}\end{aligned}`.