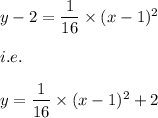Question

Using a directrix of y = −2 and a focus of (1, 6), what quadratic function is created?

Answer 1

(x-h)²=4p(y-k), the focus is (h, k+p), the directrix is y=k-p
in this case, h=1, k+p=6, k-p=-2, so k=2, p=4
so the equation is (x-1)²=16(y-2)

Answer 2

The quadratic function which is created is:

`y=(1)/(16)* (x-1)^2+2`

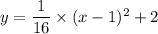
Explanation:

We know that if the equation of the parabola is given by:

`(x-h)^2=4p(y-k)`

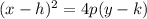
where the focus of the parabola is: (h,k+p)

and the equation of the directrix is given by: y=k-p

Here the focus of the parabola is at: (1,6)

i.e. (h,k+p)=(1,6)

i.e. h=1---------(1) and k+p=6--------(2)

And the equation of directrix is: y= -2

i.e. k-p= -2---------(3)

On using equation (2) and (3) we have:

2k=4

and k=2

and putting the value of k in equation (2) we have:

p=4

Hence, the quadratic function is given by:

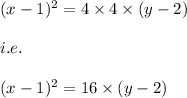
`(x-1)^2=4* 4* (y-2)\\\\i.e.\\\\(x-1)^2=16* (y-2)`

i.e.

`y-2=(1)/(16)* (x-1)^2\\\\i.e.\\\\y=(1)/(16)* (x-1)^2+2`