Answer:
Radical form refers to a form of an algebraic expression in which we have a number or an expression underneath a radical.
Any algebraic expression involving exponents then, we can write it in radical form based on the fact that
 is equivalent to the nth root of
is equivalent to the nth root of
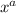 i.e,
i.e,
 =
=
![\sqrt[n]{x^a}](https://img.qammunity.org/2019/formulas/mathematics/high-school/3mtopcv8rg8n0a7yngm0aqeof2thz7xjpa.png)
Now, Consider the expression:
![4^{(1)/(7)} = \sqrt[7]{4}](https://img.qammunity.org/2019/formulas/mathematics/high-school/huu78lfj7394h4zb9dipqa890eamzr8sog.png)
![4^{(7)/(2)} = \sqrt[2]{4^7}](https://img.qammunity.org/2019/formulas/mathematics/high-school/faqauhuhok4gat8o0nsm6g5hb1tgjej940.png)
![7^{(1)/(4)} = \sqrt[4]{7}](https://img.qammunity.org/2019/formulas/mathematics/high-school/5bx8fdua2psbb8s9bu5gz0oraan4w468sj.png)
![7^{(1)/(2)} = \sqrt[2]{7}](https://img.qammunity.org/2019/formulas/mathematics/high-school/zsiv8wgvmx383ho2favy59d8enk4ophrxn.png)