The first term of an arithmetic sequence is 14, that is:
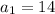
. Also, we are given that the common difference is 9, which means that each next term is obtained by adding 9, as follows:
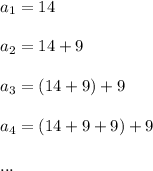
.
So we notice that to get the value of the n'th term,

, we must add (n-1) nines to 14.
(For example, to find the second term we added 1 nine to 14. To find the third term we added 2 nines to 14, and so on...)
Thus,

Answer: 104.