Question

This table shows the daily high temperature, in Fahrenheit, for two cities for ten days. City A 90 85 84 85 80 82 83 85 89 82 City B 77 78 98 91 78 76 78 85 84 71 Which conclusion can be drawn from the data?

Answer 1

Since the person didn't write the answer choices they were:

A. On average, city A was warmer than city B.

B. The median and mode are different for city B.

C. The temperature range between the maximum and minimum values for city A is greater than the temperature range between the maximum and minimum values for city B.

D. The median is less for city A than for city B.

I believe it is A personally cause i took the test and got it right

Answer 2

1. On average city A is warmer than city B
2. The median and mode are same for city B.
3. The temperature range between the maximum and minimum values for city B is greater than the temperature range between the maximum and minimum values for city A.
4. The median is less for city B than for city A.

Explanation:

We are given the following information in the question:

City A: 90 85 84 85 80 82 83 85 89 82

City B: 77 78 98 91 78 76 78 85 84 71

Formula:

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Median:\\\text{If n is odd, then}\\\\Median = \displaystyle(n+1)/(2)th ~term \\\\\text{If n is even, then}\\\\Median = \displaystyle((n)/(2)th~term + ((n)/(2)+1)th~term)/(2)`

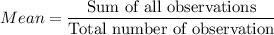
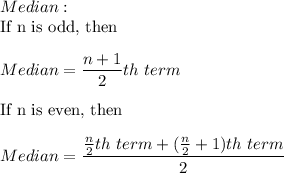
Mode is the most frequent observation

City A:

`Mean =\displaystyle(845)/(10) = 84.5`

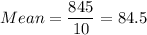
Median:

Sorted data: 80, 82, 82, 83, 84, 85, 85, 85, 89, 90

Median =
`(84+85)/(2) = 84.5`

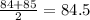
Mode = 85

Minimum = 80

Maximum = 90

Range = Maximum - Minimum = 10

City B:

`Mean =\displaystyle(816)/(10) = 81.6`

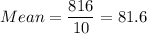
Median:

Sorted data: 71, 76, 77, 78, 78, 78, 84, 85, 91, 98

Median =
`(78+78)/(2) = 78`

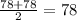
Mode = 78

Minimum = 71

Maximum = 98

Range = Maximum - Minimum = 27

Thus, we can say that:

• On average city A is warmer than city B
• The median and mode are same for city B.
• The temperature range between the maximum and minimum values for city B is greater than the temperature range between the maximum and minimum values for city A.
• The median is less for city B than for city A.