Answer:
(3,0) the graph touches the x-axis
Explanation:
the graph of
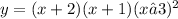
we need to check what happens to the graph near the point (3,0)
In f(x) we have (x-3)^2
LEts plug in 3 for x and check

y=0, so (3,0) is one of the zero of the given f(x)
In f(x) we have
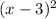
Exponent is 2 that is even. It means the multiplicity is even.
When the multiplicity is even then the graph touches the x axis but does not cross x axis
So at (3,0) the graph touches the x-axis