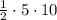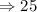In isosceles right triangle ABC, point is on hypotenuse \overline{BC} such that \overline{AD} is an altitude of \triangle ABC and DC = 5. What is the area of triangle ABC?

Question

asked Sep 8, 2019 108k views

1 Answer

Tacticalmovephase · Answer 1 · 2019-09-12T21:56:10+0000

Answer:

Area of triangle is 25.

Explanation:

We have been given an isosceles right triangle

Isosceles triangle is the triangle having two sides equal.

Figure is shown in attachment

By Pythagoras theorem

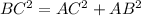
BC^2=AC^2+AB^2

AD is altitude which divides the triangle into two parts

DC=5 implies BC =10 since D equally divides BC

Let AC=a implies AB=a being Isosceles

On substituting the values in the Pythagoras theorem:

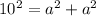
10^2=a^2+a^2

100=2a^2

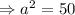
$\Rightarrow a^2=50$

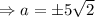
$\Rightarrow a=\pm5√(2)$

WE can find area of right triangle by considering height AB and AD

Area of triangle ABC is:

$(1)/(2)\cdot BC\cdot AD$ (1)

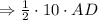
$\Rightarrow (1)/(2)\cdot 10\cdot AD$

And other method of area of triangle is:

$(1)/(2)\cdot AB\cdot BC$ (2)

Equating (1) and (2) we get:

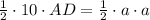
$(1)/(2)\cdot 10\cdot AD=(1)/(2)\cdot a\cdot a$

$\Rightarrow AD=(a^2)/(10)$

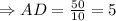
$\Rightarrow AD=(50)/(10)=5$

Using area of triangle is:
$(1)/(2)\cdot BC\cdot AD$

Now, the area of triangle ABC=
$(1)/(2)\cdot 5\cdot 10$

$\Rightarrow 25$