Question

What is the solution to the following system? 3x+3y=10
-9x-9y=-30

Answer 1

Infinite Solution

Explanation:

Given :

`3x+3y=10` -----(A)

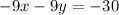`-9x-9y = -30` ------(B)

To Find : Solution of the given system of equations

Solution :

We will solve it by using substitution method

Finding the value of x from equation (B)

⇒
`-9x-9y = -30`

⇒
`-9x= -30+9y`

⇒
`x= (-30+9y)/(-9)`

⇒
`x= (-10+3y)/(-3)`

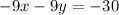
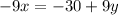
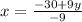
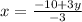
Putting this value of x in equation (B)

⇒
`3( (-10+3y)/(-3))+3y=10`

⇒
`10-3y+3y = 10`

⇒
`10= 10`

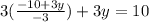
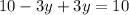
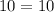
Since x and y both gets eliminated from the equation we got 10 = 10

Since the equations represent the same line.

If a consistent dependent system that has an infinite number of solutions

Hence there is infinite solution .

Answer 2

Infinite number of solutions.

Explanation:

We have the equations,

1. 3x+3y=10

2. -9x-9y= -30

Now, if we multiply equation 1 with -3, we will obtain equation 2.

i.e. -3×(3x+3y)= -3×10

i.e. -9x-9= -30

So, we see that both the equations are same.

The equation 3x+3y=10 will have solution for many values of x and y.

Hence, the system will have infinite number of solutions.