Question

Solve algebraically: x2 − x ≥ 6.

A. x ≥ 3 and x ≥ −2
B. x ≥ 3 or x ≤ −2
C. x ≤ 3 and x ≤ −2
D. x ≤ 3 or x ≥ −2

Answer 1

B. x ≥ 3 or x ≤ −2

Explanation:

Inequalities

Solve the inequality:

`x^2-x\ge 6`

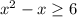
Subtracting 6:

`x^2-x-6\ge 0`

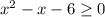
Factoring:

(x-3)(x+2) ≥ 0

We have a product that must be greater or equal to 0. This can only happen if:

x - 3 ≥ 0 and x + 2 ≥ 0

Or:

x - 3 ≤ 0 and x + 2 ≤ 0

The first couple of conditions yields to:

x ≥ 3 and x ≥ -2

Which lead to the solution

x ≥ 3 [1]

The second couple of conditions yields to:

x ≤ 3 and x ≤ -2

Which lead to the solution

x ≤ -2 [2]

The final solution is [1] or [2]:

Answer:

B. x ≥ 3 or x ≤ −2