Question

Please help with this ...Its very urgent..

Answer 1

sorry if it's a little bit ugly

Answer 2

Answer: q²x² - p³x + 3pqx + q = 0

Explanation:

Since a and B are the roots of x² - px + q = 0, then x = a and x = B

⇒ (x - a)(x - B) = 0

⇒ x² - ax - Bx + aB = 0

⇒ x² - (a + B)x + aB = 0

Comparing this to the given equation of x² - px + q = 0, we discover that

• p = a + B
• q = aB

Next, given the roots for the new equation as
`x = (a)/(B^2) \quad\text{and}\quad\ x=(B)/(a^2)`

⇒
`\bigg(x - (a)/(B^2)\bigg)\bigg(x-(B)/(a^2)\bigg)=0`

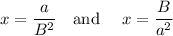
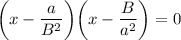
⇒ (B²x - a)(a²x - B) = 0

⇒ a²B²x² - a³x - B³x + aB = 0

⇒ a²B²x² - (a³ + B³)x + aB = 0

Let's look at each term individually:

1st term: a²B²x² = (aB)²x² = q²x² (since q = aB)

2nd term: (a³ + B³)x cubic formula can be used

= [(a + B)(a² - aB + B²)]x

= [(a + B)(a² + (2aB - 3aB) + B²)]x

= [(a + B)(a² + 2aB + B² - 3aB)]x

= [(a + B)(a + B)² - 3aB)]x

= [( p )( p² - 3 q )]x since p = a + B and q = aB

= (p³ - 3pq)x distributed "p" into p² - 3q

= p³x - 3pqx distributed "x" into p³ - 3pq

3rd term: aB = q since q = aB

Put it all together:

q²x² - (p³x - 3pqx) + q = 0

⇒ q²x² - p³x + 3pqx + q = 0