Question

Help!!!!!!!!!!!!

Given that cosΘ = 3/2
and that Θ lies in quadrant IV, determine the value of sinΘ.

A) -1/2

B) 1/2

C) square root 2/2


D) square root 3/2

Answer 1

- 1/ 2

Step-by-step explanation

-1\ 2

Use the Pythagorean identity, sin2Θ + cos2Θ = 1 to get sinΘ = ±1 - cos2Θ, then solve for sinΘ.

Answer 2

None of the Above

Explanation:

As it is given that

cosФ= 3/2

and Ф lies in quadrant 4

Now in quadrant 4 we know that by the rules of trigonometry that

cos Ф is positive in 4th quadrant also in 4th quadrant

and sinФ is negative in 4th quadrant

also we know that by simple rules of trigonometry in a right angled triangle

cos Ф=
`(Base)/(Hypotenuse)` =
`(3)/(2)`

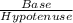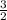
now from the law of trigonometry

cos²Ф+sin²Ф=1

From this we derive the value of sinФ

solving the equation

sin²Ф=1-cos²Ф

Putting in the values of cos Ф

sin²Ф=1-
`((3)/(2))^(2)`

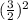
sin²Ф=1-
`((9)/(4))`

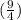
solving the fraction

sin²Ф=
`((4-9)/(4))`

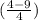
sin²Ф=
`((-5)/(4))`

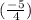
so taking square root of both sides

`\sqrt{sin^(2)\alpha}=\sqrt{(-5)/(4) }`

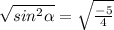
here

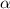`\alpha`=Ф

so it becomes

sin Ф=
`(√(-5) )/(2)`

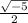
as we know that in imaginary numbers

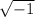`√(-1)` = ι

so the given becomes

sin Ф=
`\frac{{-5ι} }{2}`

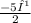
Which is the value of sin Ф

And in the given values we can see that it is none of the values

Also seeing the question we can see that the question is absurd because

cos Ф= base / hypotenuse

in our question we can see that base =3 and hypotenuse = 2

but in real geometry this is the rule that hypotenuse can never be smaller then base either it is equal to base or greater then base

the formula for finding value of finding hypotenuse is

hypotenuse ² = base ² + perp ²

so this formula shows that if perp is 0 then hypotenuse will be equal to base

in other cases it would be greater then base