Solution:
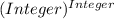
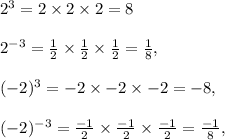
In all cases we are getting an integer.
So, yes, Marcus is correct.
Option D : Marcus is correct. If any integer is raised to any integer exponent, the base is multiplied times the exponent. The product of two integers is always a rational number.