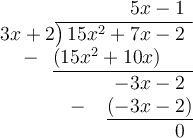1 Answer

Ask a Question

Nevin Thomas · Answer 1 · 2023-10-04T10:22:38+0000

Answer:

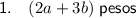
$\textsf{1.} \quad (2a+3b)\; \sf pesos$

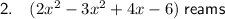
$\textsf{2.} \quad (2x^2-3x^2+4x-6)\; \sf reams$

$\textsf{3.} \quad (5x-1)\; \sf km/h$

Explanation:

Dividend : A number/expression that is divided by the divisor.

Divisor : The number/expression that divides the dividend.

Quotient : The result obtained by the division.

Remainder : The number/expression left behind.

Long division method

Divide the first term of the dividend by the first term of the divisor, and put that in the answer.
Multiply the divisor by that answer, put that below the dividend.
Subtract to create a new dividend.
Repeat.

The solution is the quotient plus the remainder divided by the divisor.

Question 1

Using long division:

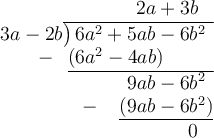
$\large \begin{array}{r}2a+3b\phantom{))}\\3a-2b{\overline{\smash{\big)}\,6a^2+5ab-6b^2\phantom{)}}}\\{-~\phantom{(}\underline{(6a^2-4ab)\phantom{-b)..)}}\\9ab-6b^2\phantom{)}\\-~\phantom{()}\underline{(9ab-6b^2)\phantom{}}\\0\phantom{))}\end{array}$

Question 2

Using long division:

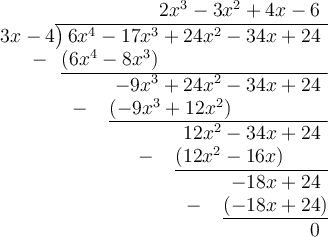
$\large \begin{array}{r}2x^3-3x^2+4x-6\phantom{)}\\3x-4{\overline{\smash{\big)}\,6x^4-17x^3+24x^2-34x+24\phantom{)}}}\\{-~\phantom{(}\underline{(6x^4-8x^3)\phantom{-bbbbbbbbbbbbbbbbb.)}}\\-9x^3+24x^2-34x+24\phantom{)}\\-~\phantom{()}\underline{(-9x^3+12x^2)\phantom{bbbbbbbbbbb.}}\\12x^2-34x+24\phantom{)}\\-~\phantom{()}\underline{(12x^2-16x)\phantom{bbbb..}}\\-18x+24\phantom{)}\\-~\phantom{()}\underline{(-18x+24)}\\0\phantom{)}\end{array}$

Question 3

Using long division:

$\large \begin{array}{r}5x-1\phantom{)}\\3x+2{\overline{\smash{\big)}\,15x^2+7x-2\phantom{)}}}\\{-~\phantom{(}\underline{(15x^2+10x)\phantom{-b)}}\\-3x-2\phantom{)}\\-~\phantom{()}\underline{(-3x-2)\phantom{}}\\0\phantom{)}\\\end{array}$

0 Comments

Your comment on this question:

Your answer

1 Answer

Question 1

Question 2

Question 3

0 Comments

Your comment on this answer:

Other Questions