Question

Which function is graphed below?

Answer 1

which one was it

Explanation:

Answer 2

The correct option is C. The given graph represents the function f(x)=sin(x).

Explanation:

From the given graph it is clear that the initial value of the function is 0.

The maximum value of function is 1 at
`x=(\pi)/(2)`.

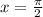The minimum value of function is -1 at
`x=(3\pi)/(2)`.

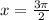The period of the function is 2π.

The x-intercepts are 0, π, 2π.

These are the properties of a positive sine function. The given graph represents the function f(x)=sin(x).

Therefore the correct option is C.

To confirm the solution find the value of each function at x=0, and
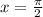`x=(\pi)/(2)`. The function must be satisfy by the points (0,0) and
`((\pi)/(2),1)`

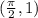
For option (1),

`f(x)=-\cosx`

`f(0)=-\cos(0)=-1\\eq 0`

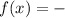
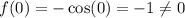
Therefore option 1 is incorrect.

For option (2),

`f(x)=\cosx`

`f(0)=\cos(0)=1\\eq 0`

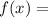
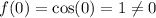
Therefore option 2 is incorrect.

For option (3),

`f(x)=\sinx`

`f(0)=\sin(0)=0`

`f((\pi)/(2))=\sin((\pi)/(2))=1`

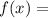
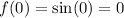
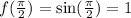
Therefore option 3 is correct.

For option (4),

`f(x)=-\sinx`

`f(0)=-\sin(0)=0`

`f((\pi)/(2))=-\sin((\pi)/(2))=-1\\eq 1`

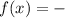
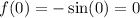
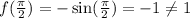
Therefore option 4 is incorrect.