Question

The function f(x)=x(200-x) models the area of a pasture, in square yards, as a function of its length. Which are possible lengths of the pasture? 125 yards 200 yards 170 yards 225 yards 210 yards

Answer 1

(a): x = 125 yards.

(c): x = 170 yards.

Explanation:

Given

`f(x) = x(200 - x)`

`x = length\\\\`

`f(x) = area`

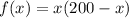
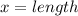
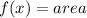
Required

Determine the possible length

For a length to be possible or usable, the calculated area must be greater than 0.

(a): x = 125 yards.

`f(x) = x(200 - x)`

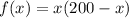
Substitute 125 for x

`f(125) = 125 * (200 - 125)`

`f(125) = 125 * 75`

`f(125) = 9375`

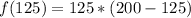
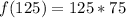
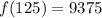
(b): x = 200 yards.

`f(x) = x(200 - x)`

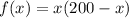
Substitute 200 for x

`f(200) = 200 * (200 - 200)`

`f(200) = 200 * 0`

`f(200) = 0`

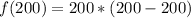
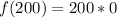
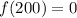
(c): x = 170 yards.

`f(x) = x(200 - x)`

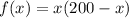
Substitute 170 for x

`f(170) = 200 * (200 - 170)`

`f(170) = 200 * 30`

`f(170) = 6000`

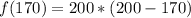
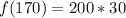
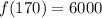
(d): x = 225 yards.

`f(x) = x(200 - x)`

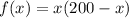
Substitute 225 for x

`f(225) = 200 * (200 - 225)`

`f(225) = 200 * (- 25)`

`f(225) = -5000`

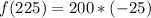
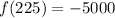
(e): x = 210 yards.

`f(x) = x(200 - x)`

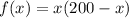
Substitute 210 for x

`f(220) = 200 * (200 - 210)`

`f(220) = 200 * (- 10)`

`f(220) = -2000`

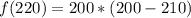
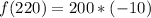
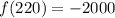
From the above calculations, only values of x that are 125 and 170 makes the function true