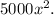Answer: The fourth term is
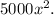
Step-by-step explanation: We are given to find the fourth term in the expansion of the following binomial :
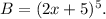
We know that
the r-th term in the expansion of the binomial
 is given by
is given by
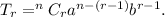
For the given term, we have
n = 5 and r = 4.
Therefore, fourth term is given by
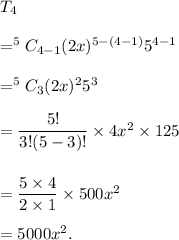
Thus, the fourth term is