Answer:
D)80,000; exponential function
Explanation:
We are given that a town with a population of 10,000 doubles every 14 years
So, Initial Population = 10,000
Now we are given that what will the population be in 42 years
First determine how many times population will double :
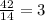
So, In 42 years it doubles three times .
Now Linear functions change at a constant rate per unit interval while An exponential function changes by a common ratio over equal intervals.
So, the given situation will be modeled by exponential function
So, Using exponential function :
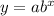
Where a is Initial Population = 10,000
b is rate of change
x = time = 3 times
So, the population will be in 42 years=

=
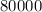
So, the population will be 80,000 after 42 years.
Thus Option D is correct.
D)80,000; exponential function