Question

90 POINTS MATH

Find the range of possible values for the variable. Show work.

Final Answer
_______ < y < ________

Answer 1

1.25 < y <= 8.32124

Explanation:

We use the law of cosines for two triangles:

`c^2 = a^2 + b^2 - 2 a b \cos(\gamma) \\ d^2 = a^2 + b^2 - 2 a b \cos(\delta)`

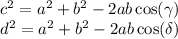
This answer shows how to use the Reduce and Exists functions of Mathematica to solve either this problem, or the general problem of a pair of triangles with two sides of one triangle equal to two sides of the other triangle. That answer (with
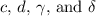`c,\, d,\, \gamma,\, \text{and}\ \delta` as independent variables which must be given ranges) has 11 cases, and would be a terrible waste of time to find by hand.

The law of cosines is used twice, with the same values for a and b, but different values for c and γ . Here I use the constants
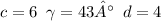`c = 6\,\ \gamma = 43°\, \ d = 4`. The following equations and inequalities are supplied to Reduce, with an Extential quantifier specifying that Reduce should discover the range of values for
`\cos(\gamma)`.

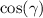`\text{problem}=\exists _{\{a,b\}}\left(\begin{array}{ccc}36=a^2+b^2-2 a b \cos (43 {}^(\circ))\ \ \land\\16=a^2+b^2-2 a b \cos (\delta )\,\,\land\\ 0<a\land 0<b\land -1<\cos (\delta )<1\end{array}\right)\\ \\ \text{variables}=\{a,b,\cos (\delta )\}\\ \\ \text{red}=\text{Reduce}[\text{problem},\text{variables},\mathbb{R}]\,\,\,\,\,\text{gives}\,\,\,\,\,(1)/(9) (4 \cos (43 {}^(\circ))+5)\leq \cos (\delta )<1\\\\\text{N}[\text{red}]\,\,\,\text{gives}\,\,\,0.880602\leq \cos (\delta )<1.`

This proves (since we used Reduce, not Solve, which is less reliable) that

• a triangle exists that has angle 43°, two adjacent sides of length a and b and opposite side of length 6, and that

• a second triangle exists with unknown angle, adjacent sides a and b equal to the corresponding sides of the first triangle, and opposite side length 4.

• There is only one range of angles which satisfy the requirements.

`\text{mincos}=\text{First}[\text{red}]\ \ \text{gives}\ \ (1)/(9) (4 \cos (43 {}^(\circ))+5)\\\text{maxcos}=\text{Last}[\text{red}]\ \ \text{gives}\ \ 1\\\\\text{Solve}[4 y-5=\delta,y ]\ \ \ \text{gives}\ \ \ \left\{\left\{y\to (\delta )/(4)+(5)/(4)\right\}\right\}\\ \\\\\ (5)/(4)<y\leq (1)/(4) \left(\frac{\cos ^(-1)}{{{}^(\circ)}}\left((1)/(9) (4 \cos    (43 {}^(\circ))+5)\right)}+5\right)`

Answer 2

1.25 < y < 8.32124...

Explanation:

The least y can be is the value that makes the angle in the smaller triangle be zero. (This condition will exist when the difference of side lengths is 4.)

... 4y -5 = 0

... y = 5/4 . . . . . add 5, divide by 4.

_____

The greatest y can be is the value obtained when the triangle is isosceles. For the larger triangle, that makes the side lengths (s) be ...

... 3/s = sin(43°/2)

... s = 3/sin(21.5°)

Then for the smaller triangle, that makes the angle be ...

... 4y -5 = arcsin(2/s) = arcsin(2/3·sin(21.5°))

... y = 1.25 + arcsin(2/3·sin(21.5°))/4

... y ≈ 8.32124