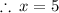Question

Two problems here I need solved! I need every step, so please have that with your answers!!

1. Solve this rational equation:


`(1)/((x-4))+(x)/((x-2))=(2)/(x^(2)-6x+8)`


1. Solve this radical equation:


`√(x+11) -x=-1`

Answer 1

QUESTION 1

We want to solve,


`(1)/((x-4))+(x)/((x-2))=(2)/(x^(2)-6x+8)`

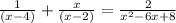
We factor the denominator of the fraction on the right hand side to get,


`(1)/((x-4))+(x)/((x-2))=(2)/(x^(2)-4x - 2x+8).`

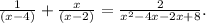
This implies

`(1)/((x-4))+(x)/((x-2))=(2)/(x(x-4) - 2(x - 4)).`


`(1)/((x-4))+(x)/((x-2))=(2)/((x-4)(x - 2))`

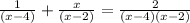
We multiply through by LCM of

`(x-4)(x - 2)`


`(x - 2) + x(x-4) = 2`

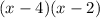
We expand to get,


`x - 2 + {x}^(2) - 4x= 2`

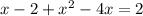
We group like terms and equate everything to zero,


`{x}^(2) + x - 4x - 2 - 2 = 0`

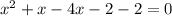
We split the middle term,


`{x}^(2) + - 3x - 4 = 0`

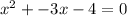
We factor to get,


`{x}^(2) + x - 4x- 4 = 0`


`x(x + 1) - 4(x + 1) = 0`


`(x + 1)(x - 4) = 0`


`x + 1 = 0 \: or \: x - 4 = 0`


`x = - 1 \: or \: x = 4`

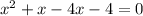
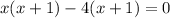
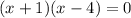
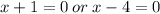
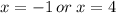
But

`x = 4`
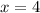
is not in the domain of the given equation.

It is an extraneous solution.


`\therefore \: x = - 1`
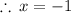
is the only solution.

QUESTION 2


`√(x+11) -x=-1`

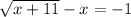
We add x to both sides,


`√(x+11) =x-1`

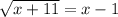
We square both sides,


`x + 11 = (x - 1)^(2)`

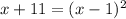
We expand to get,


`x + 11 = {x}^(2) - 2x + 1`

This implies,


`{x}^(2) - 3x - 10 = 0`

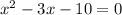
We solve this quadratic equation by factorization,


`{x}^(2) - 5x + 2x - 10 = 0`


`x(x - 5) + 2(x - 5) = 0`


`(x + 2)(x - 5) = 0`


`x + 2 = 0 \: or \: x - 5 = 0`


`x = - 2 \: or \: x = 5`

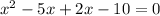
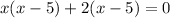
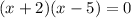
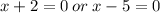
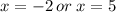
But

`x = - 2`
is an extraneous solution


`\therefore \: x = 5`