Question

A string of a kite is 100 meters long and it makes an angle of 60° with horizontal. Find the height of the kite and then find the ground distance from the kite to the person flying the kite,assuming that there is no slack in the string.

1. Draw a figure for the information given in the problems.

2. Using the correct trig function, write out the mathematical problem.

3. Solve the problem to find the missing sides.

Answer 1

The height of the kite and the distance from kite to person are 86.6 meters and 50 meters respectively.

Using Trigonometry concept ;

The height of the kite , y can be obtained thus ;

• Sine = opposite / Hypotenus

Sin(60°) = y / 100

y = sin(60°) × 100

y = 86.6 meters

B.)

The distance from the kite to the person would be ;

• Tangent = opposite / Adjacent

Tan(60) = 86.6667 / x

d = 86.6667 / Tan(60)

d = 50 meters

Therefore, the height of the kite and the distance from kite to person are 86.6 meters and 50 meters respectively.

Answer 2

Height of the kite is
`=50 √(3)` meters.

Ground distance from the kite to the person flying the kite is 50 meters.

Explanation:

Given that a string of a kite is 100 meters long and it makes an angle of 60° with horizontal.

Which mans we are getting a shape of right angle triangle as shown in picture. Where "y" is the height of the kite and "x" is the ground distance from the kite to the person flying the kite. Now we can use trigonometric ratios to find the values of x and y.

`\sin\left(60^o\right)=(\left[opposite\right])/(\left[hypotenuse\right])=(y)/(100)`

`\sin\left(60^o\right)=(y)/(100)`

`(√(3))/(2)=(y)/(100)`

`(√(3))/(2)*100=y`

`50 √(3)=y`

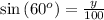
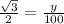
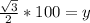
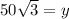
Hence height of the kite is
`=50 √(3)` meters.

similarly:

`\cos\left(60^o\right)=(\left[adjcent\right])/(\left[hypotenuse\right])=(x)/(100)`

`\cos\left(60^o\right)=(x)/(100)`

`(1)/(2)=(x)/(100)`

`(1)/(2)*100=x`

`50=x`

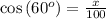
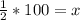
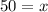
Hence ground distance from the kite to the person flying the kite is 50 meters.