Question

The heights of two cylinders are in the ratio 3:1 if the volumes of two are same find the ratio of their respective radii

Answer 1

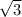`√(3)` :1

Explanation:

Ratio of height of two cylinders are 3:1

Let C2 has the height x

then height of C1 is 3x

Let r1 is the radius of C1

and r2 is the radius of C2

As given that volume of both are equal

Also we know that formula for the volume of the cylinder is

V= π r²h

for C1

V= π (r1)²h

for C2

V=π (r2)²h

As volume of both are same so equating them

π (r1)²h1 = π (r2)²h2

as h1 =3x and h2=x

putting values

π (r1)²(3x) = π (r2)²(x)

cancelling out π and x from both side of the equation

3(r1)²= (r2)²

Taking square root of both sides give

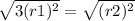
`\sqrt{3(r1)^(2) }=\sqrt{(r2)^(2) }`

r1 (
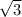`√(3)`) = r2

or

r1 : r2 =
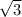`√(3)` :1