c = cost of a cookie
b = cost of a brownie
(idk if u should put the variable in front of the number, but I'm putting it after)
10c + 3b = 11.25
6c + 9b = 15.75
Isolate one of the variables of one of the equations, and substitute it into the other equation.
I will isolate "c" in the first equation
10c + 3b = 11.25 Subtract 3b on both sides
10c = 11.25 - 3b Divide 10 on both sides
c = 1.125 -
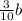or c = 1.125 - 0.3b
Now substitute this into the second equation
6c + 9b = 15.75 Since c = 1.125-0.3b, u can plug in (1.125-0.3b) for c
6(1.125 - 0.3b) + 9b = 15.75 Distribute 6 into (1.125 - 0.3b)
6.75 - 1.8b + 9b = 15.75 Combine like terms
6.75 + 7.2b = 15.75 Subtract 6.75 on both sides
7.2b = 9 Divide 7.2 on both sides
b = 1.25 $1.25
You could continue to find "c"
Since you know "b", you can plug it into one of the equations:
10c + 3b = 11.25
10c + 3(1.25) = 11.25
10c + 3.75 = 11.25
10c = 7.5
c = 0.75
PROOF
6(0.75) + 9(1.25) = 15.75
4.5 + 11.25 = 15.75
15.75 = 15.75
10(0.75) + 3(1.25) = 11.25
7.5 + 3.75 = 11.25
11.25 = 11.25