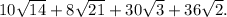Answer: The required product is
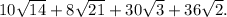
Step-by-step explanation: We are given to find the following product :
P = (2 square root 7+3 square root 6)(5 square root 2+4 square root 3).
We will be using the following property of radicals :
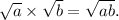
The given product can be written and evaluated as follows :
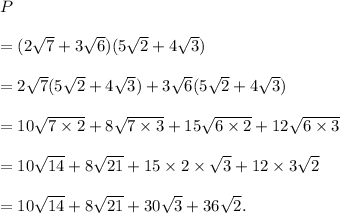
Thus, the required product is