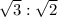Question

Satellite A orbits the earth at a height 2.00 times the earth's radius.Satellite B orbits the earth at a height 3.00 times the earth's radiusWhat is the ratio of the period of Satellite B to the period of Satellite A?

Answer 1

Answer:
`\sqrt 3 :\sqrt 2`

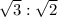
From Kepler's law: The cube of radius of the orbit of satellite is proportional to square of time period of orbit.

`r^3=(T^2 Gm)/(4\pi ^2)`

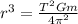
where, r is the radius of the orbit of satellite, T is the time period of satellite, G is the gravitational constant, m is the mass of the planet.

R is the radius of Earth.

`(r_A^3)/(r_B^3) = (T_A^2)/(T_B^2) \\ \Rightarrow (2R)/(3R)=(T_A^2)/(T_B^2) \Rightarrow (T_B)/(T_A)=\sqrt{(3)/(2)}`

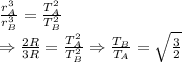
Hence, the ratio of the period of Satellite B to the period of Satellite A is
`\sqrt 3 :\sqrt 2`